什么是自动微分

在数值优化算法中，经常需要用到函数的导数。为了计算出一个函数的导数，通常有两种方法：

符号微分，简而言之就是让机器像人一样，根据一套有限的函数求导法则，对函数表达式进行变换，得出最终的表达式，从而计算出导数。常见的符号计算系统有 Mathematica；还有 SymPy ，这是一个用于符号计算的 Python 的库。数值微分，则是根据函数的泰勒展开，使用有限差分法估得导数。

无论是符号微分还是数值微分，都有他们的缺陷。符号微分必须要显示地知道函数的表达式，而且当表达式过于复杂时，计算代价很高。而数值微分则受限于机器的浮点精度，会产生较大的误差。

自动微分，简称 AD，是 Automatic Differentiation 或者Algorithmic Differentiation 的缩写。它是与符号微分、数值微分完全不同的求导方法，既不会产生很高的计算代价，也不会带来额外的误差。它的核心思想有两点：

  1. 所有函数都是简单函数的复合；
  2. 根据链式法则，对函数的求导可以被分解为对简单函数求导的复合。

下面分别介绍自动微分对一元函数、多元函数与向量函数的求导过程。

一元函数的微分

给定可微函数 $f(x):\mathbb{R}\rightarrow\mathbb{R}$，其微分 $df(x)=f'(x),dx$。其中 $f'(x)$ 是 $f$ 关于 $x$ 的导数。若 $x$ 是关于 $t$ 的可微函数 $x(t):\mathbb{R}\rightarrow\mathbb{R}$，则根据链式法则有 $$\frac{df(x)}{dt}=\frac{df(x)}{dx}\frac{dx(t)}{dt}=f'(x)x'(t)$$

举个例子。有 $f(x)=x^2$，$x(t)=t+1$，要求 $f$ 在 $t=1$ 处的导数。其各变量依赖关系如下

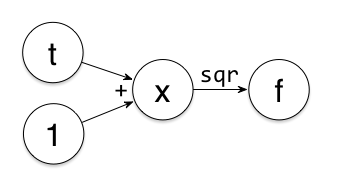
从左往右，我们分别得到 $t=1$，$x=t+1=2$，$\frac{dx}{dt}=1$，$f=x^2=4$，$\frac{df}{dx}=2x=4$，因此 $f$ 在 $t=1$ 处的导数为 $\frac{df}{dt}=\frac{df}{dx}\frac{dx}{dt}=4\times 1=4$。

看上去很简单是不是。自动微分的关键，就在于首先把函数分解为几个简单函数的复合，在这里就是加法与平方两种运算；然后再为每种简单函数定义好了导数，比如说，$t+1$ 的导数就是 $1$，而 $x^2$ 的导数就是 $2x$；最后通过对导数的组合，得到最终要求的导数。

多元函数的微分

给定可微函数 $f(\mathbf{x}):\mathbb{R}^n\rightarrow\mathbb{R}$，其微分 $df(\mathbf{x})=\nabla f(\mathbf{x})^Td\mathbf{x}$。其中 $\nabla f(\mathbf{x})$ 是 $f$ 的梯度，可以看作是广义的导数 $$\nabla f(\mathbf{x})=(\frac{\partial f}{\partial x_1},\ldots,\frac{\partial f}{\partial x_n})^T$$

把 $f$ 看作是两个函数的复合：$f(\mathbf{t}):\mathbb{R}^m\rightarrow\mathbb{R}$，$\mathbf{t}(\mathbf{x}):\mathbb{R}^n\rightarrow\mathbb{R}^m$，多元函数的链式法则是 $$\nabla_{\mathbf{x}} f(\mathbf{t}(\mathbf{x}))=\sum_{i=1}^{m}\frac{\partial f}{\partial t_i}\nabla t_i(\mathbf{x})$$

举个例子。有 $f(x,y)=(x+5)\times(x+y)$，要求 $f$ 在 $x=2$，$y=3$ 处的导数。其各变量依赖关系如下

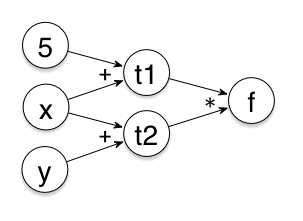
跟之前的例子类似，从左往右，我们分别得到 $t_1=x+5=7$，$t_2=x+y=5$ 与偏导数 $\frac{\partial t_1}{\partial x}=1$，$\frac{\partial t_1}{\partial y}=0$，$\frac{\partial t_2}{\partial x}=1$，$\frac{\partial t_2}{\partial y}=1$，最后有 $f=t_1\times t_2=7\times 5=35$ 与偏导数 $\frac{\partial f}{\partial t_1}=t_2=5$，$\frac{\partial f}{\partial t_2}=t_1=7$，根据 $$\frac{\partial f}{\partial x}=\frac{\partial f}{\partial t_1}\frac{\partial t_1}{\partial x}+\frac{\partial f}{\partial t_2}\frac{\partial t_2}{\partial x}=5\times 1+7\times 1=12$$ $$\frac{\partial f}{\partial y}=\frac{\partial f}{\partial t_1}\frac{\partial t_1}{\partial y}+\frac{\partial f}{\partial t_2}\frac{\partial t_2}{\partial y}=5\times 0+7\times 1=7$$ 我们有 $$\nabla f(x,y)=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})=(12,7)$$

向量函数的微分

给定可微函数 $\mathbf{f}(\mathbf{x}):\mathbb{R}^n\rightarrow\mathbb{R}^m$，其微分 $d\mathbf{f}(\mathbf{x})=\nabla\mathbf{f}(\mathbf{x})^Td\mathbf{x}$。梯度 $\nabla\mathbf{f}(\mathbf{x})$ 为

$$ \nabla\mathbf{f}(\mathbf{x}) =\begin{bmatrix} \nabla f_1(\mathbf{x}) & \nabla f_2(\mathbf{x}) & \cdots \nabla f_m(\mathbf{x}) \end{bmatrix} =\begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_2}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_1} \\ \frac{\partial f_1}{\partial x_2} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_m}{\partial x_2} \\ \vdots & \vdots & & \vdots \\ \frac{\partial f_1}{\partial x_n} & \frac{\partial f_2}{\partial x_n} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix} $$

与多元函数的微分类似，只要求得每一个 $\nabla f_i(\mathbf{x})$ 即可。

实现与应用

最常见的自动微分的实现通常基于运算符重载。借助 Haskell 中的类型类（typeclass）可以很方便地实现自动微分，比如 Matt Keeter 在他的一篇博文中用 40 行左右的代码实现了自动微分，并用其解决约束求解问题。更著名的是 Edward Kmett 大神写的 ad 库，十分强大。自动微分的应用非常广泛，具体的可以参见参考资料。

参考资料